Inversion gauche/droite mais pas haut/bas, les miroirs ne feraient donc que la moitié du boulot ?
S'observer dans un miroir est une tâche quotidienne, automatique, et pourtant cela a dû vous arriver au moins une fois : vous vous êtes arrêtés, vous avez fixé votre reflet d'un œil neuf, et vous vous êtes fait la remarque, "tiens, mon reflet est un gaucher/droitier", contrairement à vous. Et là, deux possibilités. Soit vous avez poursuivi tranquillement votre toilette en souriant à l'idée de ce double parfaitement identique -à ce petit défaut près- , soit vous avez froncé les sourcils un moment en poursuivant votre réflexion un peu plus loin, et constaté : "mais par contre, il ne voit pas le monde à l'envers. Même pour lui, le sol est en bas et le plafond en haut, étrange." Du coup, vous allez même jusqu'à pencher la tête à 90° vers la droite, de sorte que dans votre champ de vision, la gauche devienne le haut, la droite devienne le bas, mais non, l'inversion constatée ne se répercute pas sur l'axe vertical. Vous restez perplexe un moment, et réalisez finalement que ce simple miroir reste bien mystérieux. Puis le quotidien reprend ses droits, sans pour autant dissiper la confusion que l'expérience vous a laissée.
Et si nous essayions de démystifier cela ? Cela sera l'occasion de comprendre précisément l'action d'un miroir, et comment se définissent naturellement les différentes directions dans l'espace physique, à trois dimensions.
Action d'un miroir
Imaginons un rayon de lumière, provenant d'une direction un peu quelconque et venant frapper le miroir. Si vous faites l'expérience, vous verrez que le rayon réfléchi reste dans le plan formé du rayon initial (nommé rayon incident) et de la perpendiculaire (appelé la normale) à la surface du miroir. Les angles, indiqués par les arcs de cercle sur le schéma ci-dessous, sont égaux.
Il existe une raison physique à cette égalité. Le faisceau de lumière peut être considéré comme un flot ininterrompu de particules, un flux de photons, qui viennent percuter le miroir. Ces collisions, nous avons déjà eu l'occasion de les décrire dans cet article sur l'énergie.
À partir des lois de conservation de l'énergie et de la quantité de mouvement, il est possible de calculer les vitesses finales v f et V f d'objets qui s'entrechoquent, si l'on connaît leurs masses m et M ainsi que leurs vitesses initiales v i et V i :
Le miroir n'est rien d'autre qu'un obstacle dont la masse M est très, très grande devant la masse d'une particule m. On en déduit que la somme m+M est très proche de M, donc le rapport est très proche de 2, et très proche de 0. De plus, le miroir est immobile, donc Vi = 0.
Ainsi,
Ce résultat indique que la particule conserve sa vitesse initiale mais est renvoyée, le signe moins indiquant qu'elle repart en sens inverse. Quant au miroir, il reste immobile. On pourra me reprocher d'appliquer ces formules pour des photons (c'est en fait un peu hasardeux), mais cette liberté me permet d'arriver au résultat sans trop m'étendre.
Point crucial : notez sur le schéma de la réflexion que ce n'est pas la direction globale du rayon qui est importante (flèche rouge). Cette direction se décompose en un déplacement perpendiculaire au miroir (flèche bleu sombre), et un déplacement parallèle au miroir (flèche bleu clair). Ce déplacement perpendiculaire est responsable de la collision, cette composante est donc inversée. En revanche, le déplacement parallèle au miroir ne joue aucun rôle.
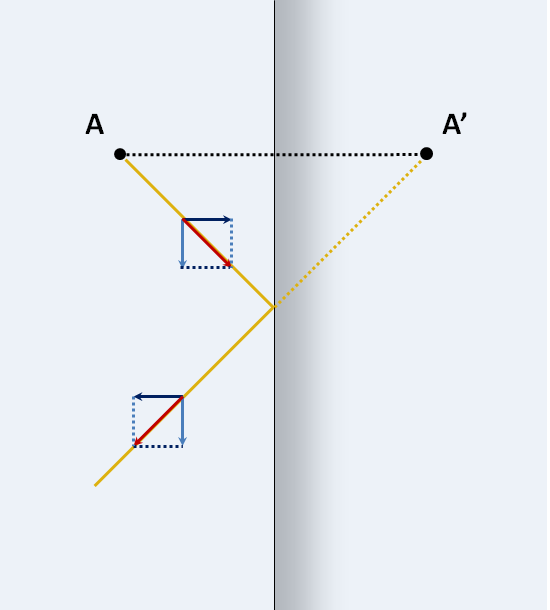
La conséquence de l'action du miroir sur le rayon lumineux est résumée sur le schéma suivant. Il s'agit d'une vue de dessus du premier schéma.
On y voit le prolongement du rayon réfléchi. Si l'on place une source de lumière au point A, le rayon réfléchi semblera toujours être émis par une image de cette source en A'. La position de A' est très simple à trouver, c'est le symétrique de A par rapport à la surface du miroir. Les distances A-miroir et miroir-A' sont égales.
C'est cette propriété qui fait du miroir ce qu'il est : il produit une parfaite copie optique de ce qu'il a en face de lui. Chaque point source possède un point image. On dit que le miroir est rigoureusement stigmatique. Reste à voir l'effet du miroir sur les directions.
On peut appliquer la symétrie à tout un ensemble de points, et en les distinguant, en déduire comment se transforment les directions. En partant à chaque fois du point noir au point rouge, on voit que :
- La direction verticale ne change pas, tout comme la direction horizontale et parallèle au miroir. Dans ces deux cas, aller du point noir au point rouge, c'est aller dans le même sens.
- En revanche, la direction perpendiculaire est inversée.
Ce que le miroir fait subir physiquement aux rayons lumineux se retrouve dans les images elles-même. Il inverse la direction perpendiculaire à sa surface.
Note : comment renvoyer à coup sûr un rayon lumineux vers sa source lorsque sa direction est quelconque ? On dispose trois miroirs en coin de cube. Dans ce cas précis, chaque miroir inverse une direction distincte, ce qui fait que la direction globale du rayon est inversée.
Ce type de réflecteur a été installé sur la Lune, afin de pouvoir renvoyer des faisceaux laser émis depuis la Terre, sans qu'il y ait de réglages d'orientation à faire. C'est grâce à cela que l'on est capable de mesurer la distance Terre-Lune (environ 400 000 km) au centimètre près...
Un ensemble de miroirs en coin de cube. Chaque ricochet du rayon lumineux inverse chacune des trois directions de l'espace (en rouge), de sorte que le rayon final est parallèle au rayon initial.
Mais au fait, comment définissons-nous les directions, concrètement ?
Cette question est bien plus riche qu'il n'y paraît, car elle n'est pas purement physique. Nous vivons dans un monde physique à trois dimensions (longueur, largeur, hauteur), il y a donc bien trois directions, mais la manière dont nous orientons ces directions est plus subtile que ce que l'on pourrait croire. Or, si cette question n'est pas éclaircie, nous risquons de nous embourber.
Finalement, comment avons-nous l'habitude de traiter les directions ? Nous nous basons sur notre champ de vision. Nous définissons quatre régions – le haut, le bas, la gauche, la droite – en ayant en tête que ce qui est observé fait partie de l'avant, et qu'il existe un arrière.
Mais à bien y réfléchir, cela ne suffit pas. Tout un ensemble d'éléments participent à notre perception des directions. Observez la pièce où vous vous trouvez et penchez la tête de 90°. Ne remarquez-vous pas que la sensation est très différente que celle que donnerait une caméra qui ferait le même mouvement ? Nos sens ne travaillent pas séparément, et au moins trois éléments sont susceptibles d'intervenir de manière plus ou moins prononcée :
- Vous savez que vous tournez la tête, vous êtes conscient du mouvement que vous exécutez.
- Vous connaissez les objets qui vous entourent, et donc interprétez leur orientation « naturelle ». Si vous voyez une étendue plane d'orientation quelconque, accolé à un meuble à quatre pieds, vous identifierez rapidement un « sol » sur lequel se tient une « table », trahissant automatiquement une orientation particulière : la table, en haut, se tient sur le sol, en bas.
Cet effet est d'autant plus clair lorsque vous voyez un tableau ou un dessin représentant quelque chose qui vous semble complètement inintelligible. Sans signification, vous avez presque envie de tourner le tableau dans tous les sens pour en trouver une. Puis, soudain, un détail vous permet de le comprendre, et là, instantanément, vous ne pouvez plus toucher son orientation : le haut et le bas se sont définis. Vous savez s'il est à l'endroit, à l'envers, penché, ou même si le cadre a été volontairement choisi incliné par rapport au sujet.
- Votre oreille interne vous indique constamment l'orientation du champ de pesanteur (au moins ses variations, dues à vos mouvements de tête).
Notre orientation dans l'espace s'appuie ainsi sur une multitude de facteurs. Et tout naturellement, ces éléments cherchent automatiquement à rétablir l'orientation réelle d'une seule direction physique : celle du champ de pesanteur, qui définit donc la verticale, le haut et le bas. C'est la seule direction qui importe vraiment, puisque notre morphologie nous oblige à nous tenir debout pour nous mouvoir correctement.
D'autre part, l'axe avant-arrière nous est aussi imposé par notre morphologie, et nous regardons vers l'avant. Ce n'est plus une direction extérieure à l'être humain, elle est au contraire intrinsèque. Enfin, c'est à partir de la verticale et de notre axe avant-arrière, que nous définissons la direction gauche-droite, elle aussi intrinsèque.
Et donc...
Deux personnes qui se font face ont leurs axes avant/arrière opposés, donc leurs axes gauche/droite sont aussi opposés : la gauche de l'un est la droite de l'autre.
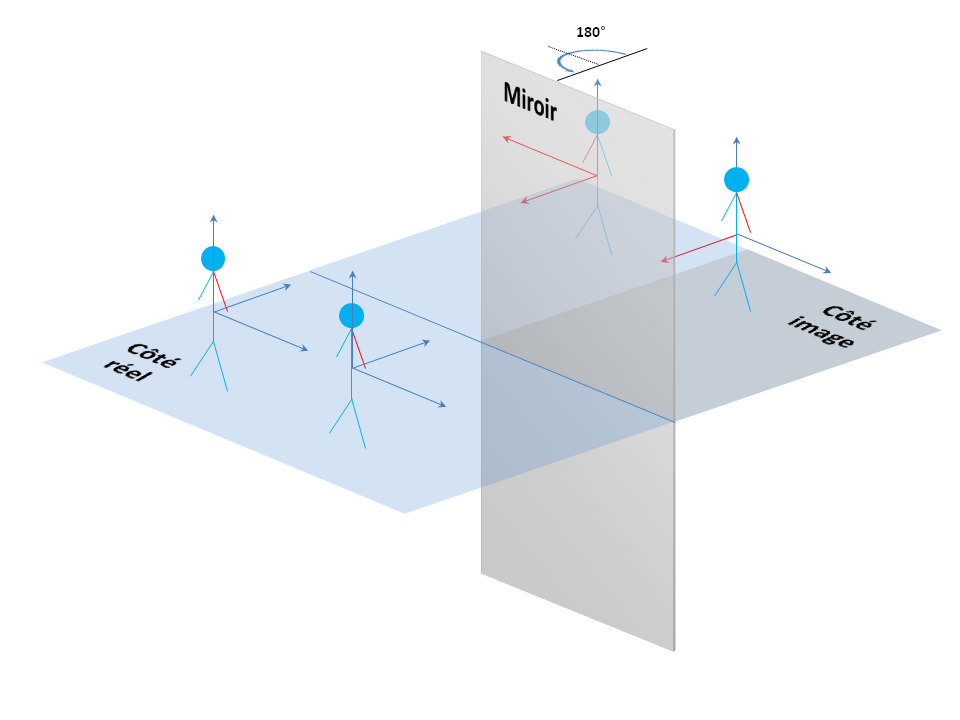
Mais la situation d'une personne face à son image est très différente, car le miroir crée un double dont l'axe avant/arrière est inversé, sans modifier ni haut/bas, ni gauche/droite. Du coup, il y a incohérence avec le cas de deux personnes qui se font face, et un droitier voit son image assimilée à un gaucher.
À gauche, deux personnes qui se font face. L'une a donc fait un demi-tour sur elle-même.
À droite, une personne et son reflet.
En rouge sont mis en évidence les axes qui ont été affectés, par rapport à l'individu original.
Fait amusant, cela est aussi vrai pour un miroir fixé au plafond ! Cette fois-ci, la direction haut/bas est inversée, la direction avant/arrière ne l'est plus, mais votre image est toujours votre opposé. Vous voyez que la gauche et la droite dépendent bien des deux autres directions, or un miroir n'en intervertit qu'une. Il faut regarder une image qui a subi deux réflexions pour retrouver un double semblable à nous-même.
On peut résumer tout cela en disant qu'une rotation de 180° n'est pas équivalente à une symétrie miroir (inversion d'un axe donné).