Peut-on dire d'une théorie physique qu'elle est vraie ou fausse ?
Sans préambule, oui. Oui, on peut répondre à la question de savoir si une théorie physique est vraie ou fausse. Mieux, on peut le faire pour toutes les théories physiques d'un seul coup : elles sont toutes fausses. Absolument toutes.
Alors quoi ? La physique ne servirait absolument à rien ? Bien au contraire ! La question, ainsi formulée, est juste mal posée. Elle renvoie à une notion de justesse et de fausseté absolues usuelles au quotidien, ou en mathématiques, lorsqu'on examine une proposition donnée. La fenêtre est-elle ouverte ou fermée ? Le nombre 12 est-il plus grand ou plus petit que 5 ? On peut répondre sans détour à ces questions, c'est l'une des possibilités ou l'autre. Dire qu'une théorie physique est rigoureusement vraie ou fausse n'a pas vraiment de sens, ou alors un sens très réducteur qui ne permet pas de comparer la valeur de deux théories distinctes. Pour le comprendre, il faut savoir comment on juge la validité d'une théorie.
Décortiquer la démarche scientifique en physique.
Vous observez un phénomène et vous voulez comprendre son origine. Pour utiliser la méthode scientifique, vous commencez par construire un modèle, c'est-à-dire une vision du monde ne comportant que les éléments que vous supposez essentiels à l'apparition du phénomène. Tout le reste est oublié. Le modèle est le support de votre théorie. Vous déduisez alors du modèle le comportement du phénomène en fonction des paramètres sur lesquels vous pouvez jouer en entrée. Pour prendre un exemple, si vous tirez à l'arc alors qu'il y a du vent, votre flèche sera déviée. En utilisant votre modèle, vous pourrez faire une prédiction de la valeur de la déviation observée en fonction, par exemple, de la vitesse du vent.
Dans un deuxième temps, vous menez une expérience en laboratoire où vous provoquez du vent à vitesse contrôlée et où vous mesurez la déviation de la flèche. Vous pouvez alors confronter théorie et expérience. Deux cas peuvent alors survenir, illustrés par les exemples suivants, lorsque l'on trace la déviation de la flèche en fonction de la vitesse du vent :
Dans le cas no1, il est clair que théorie et expérience ne collent pas. Les hypothèses contenues dans le modèle n'expliquent pas l'expérience. Il faut réessayer en partant de nouvelles hypothèses. La théorie est fausse. Dans le cas no2, tout est parfait. Les points expérimentaux et la courbe théorique se superposent parfaitement. Vous avez relié les hypothèses de départ au phénomène observé, vous savez donc d'où il provient. La théorie décrit la réalité, elle est donc vraie.
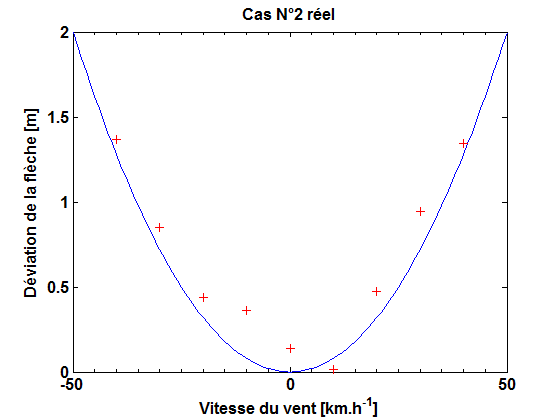
Sauf qu'il y a un problème. Un accord parfait tel qu'illustré par le cas no2 ne peut pas exister. Dans le monde réel, si je mène l'expérience déjà décrite, je ne mesurerai pas uniquement l'effet du vent. Malgré tous les efforts possibles, je ne peux pas me soustraire totalement aux conséquences des milliards (pour ne pas dire de l'infinité) d'autres phénomènes qui se produisent au moment où je livre l'expérience. Le mouvement de la Terre dans l'espace, le séisme qui frappe à mille kilomètres de là, l'effet de la lumière sur la flèche, la présence de la montagne à côté, tous ces éléments ont une contribution au résultat, aussi faible soit-elle. Donc les points expérimentaux vont forcément se répartir d'une manière analogue à celle-ci :
La théorie est donc fausse. En effet, la valeur prédite ne correspond pas à la valeur obtenue ! C'est dans ce sens que je dis que toute théorie physique est fausse.
Si je veux une théorie juste, je sais a priori, dans l'absolu, comment faire : puisque j'ai négligé des phénomènes physiques, il suffirait de les inclure dans le modèle ! Le problème est qu'inclure l'univers tout entier dans un modèle, on n'est pas prêt de le faire. Qui plus est, on ne possède pas de connaissance intégrale de l'univers, ni tous les phénomènes qui s'y produisent, puisque c'est justement pour cela qu'on pratique la science ! Donc on peut renoncer à élaborer une théorie juste.
On sent pourtant que l'histoire n'est pas terminée. Au cours du processus, n'aurait-on pas acquis quelque chose ?
Entre le cas no1 et le cas no2 réel, il y a une différence de taille : même si aucun des deux ne me permet de prédire la valeur exacte du résultat, le premier me dit tout simplement n'importe quoi tandis que l'autre me donne un résultat approché dans toutes les situations que j'ai pu tester. Autrement dit, les hypothèses que j'ai utilisées dans le second cas me permettent de deviner le comportement du phénomène. Cela veut dire que dans une certaine mesure, j'ai compris le phénomène. Je sais identifier les causes qui lui permettent de survenir.
Peut-être que pour le lecteur, le dernier graphique n'est au contraire pas satisfaisant. Plusieurs points ne suivent pas vraiment la courbe bleue, après tout. La question est de savoir si le lecteur possède suffisamment de données sur l'expérience pour pouvoir trancher. Imaginons en effet que, sans répéter l'expérience, je refasse les mesures de déviation de la flèche. Je trouverai alors des résultats différents. Pourquoi ? Parce que mesurer, c'est faire une expérience en soi. C'est comparer une référence avec ce que l'on mesure. Or, si c'est une expérience, elle subit les aléas de toutes les influences extérieures que l'on a déjà évoquées et qu'on ne peut éviter. Si l'on répète une expérience, ces influences n'ont aucune raison d'agir de la même manière que la fois précédente, donc le résultat d'une mesure sera différent d'une fois sur l'autre. Ceci n'est pas gênant, à condition d'avoir conscience de combien on se trompe. Il manque donc cette information sur les graphiques que j'ai présentés, c'est l'incertitude de mesure. Elle se représente par des barres d'erreur sur les points expérimentaux.
Imaginons que les barres d'erreurs obtenues soient celles de la figure ci-contre. La modélisation est alors tout à fait satisfaisante. La courbe théorique passe à l'intérieur de tous les domaines d'incertitude. L'expérience et la théorie sont donc compatibles : la théorie est « vraie » au sens du physicien. À ce niveau de précision, elle est jugée valide et les hypothèses qu'elle utilise suffisent à expliquer le phénomène.
L'autre cas possible vis-à-vis des barres d'erreur est illustré à gauche. Cette fois-ci, l'expérience est suffisamment précise pour montrer que la théorie développée est insuffisante pour reproduire les résultats expérimentaux. Néanmoins, la tendance générale semble la bonne (notez qu'il suffirait que l'expérience soit un peu moins précise pour retrouver le cas précédent et conclure que la théorie retranscrit bien les données). Il existe donc un ensemble de phénomènes plus fins qui modifie la tendance générale et qui ne sont pas inclus dans la théorie de base. Le modèle semble donc avoir les bonnes bases mais doit être raffiné.
Une dernière notion est la notion de domaine de validité. Supposons que théorie et expérience soient compatibles, comme sur l'avant-dernier graphique. D'après celui-ci, l'expérience a été menée pour des vents de 40 km.h-1. Et si l'on était allés plus loin ? Du point de vue théorique, il suffirait d'extrapoler la courbe bleue, qui continuerait à croître avec la vitesse du vent. Cependant, il finirait par y avoir un problème, car il est clair que pour un vent de 100-150 km.h-1, la flèche n'atteindrait même plus la cible. Le vent serait si fort que la flèche se réorienterait selon la direction du vent. Autrement dit, un phénomène négligé jusqu'alors finit par prendre suffisamment d'importance pour devenir dominant et modifier le comportement du système à l'étude. Le modèle développé avant n'est donc juste que sur une certaine gamme de valeurs des paramètres de l'expérience. Si l'on en sort, il faut raffiner le modèle. Le domaine de validité n'est pas une notion nouvelle, c'est une catégorie particulière d'hypothèses où l'on est attentif aux valeurs prises par les paramètres (si le vent n'est pas trop fort, alors je peux appliquer tel modèle). Les domaines de validité sont omniprésents. Leur existence résulte des différents rapports de force entre les « ingrédients » que l'on peut inclure dans un modèle. Il suffit souvent de changer la valeur d'un paramètre pour que la contribution négligeable d'une hypothèse devienne dominante.
Voilà, j'ai présenté le cœur de la méthode scientifique en physique. J'ai essayé de vous montrer la raison pour laquelle dire d'une théorie qu'elle est « vraie » ou « fausse » n'a pas la même signification de la bouche d'un physicien. J'insiste sur le fait que je parle des physiciens, et non des scientifiques en général : un mathématicien peut employer les mots « vrai » et « faux » dans leur sens absolu (ou « indécidable », lorsqu'une proposition ne peut être démontrée comme étant vraie ou fausse), puisqu'il s'appuie uniquement sur des constructions de l'esprit et n'a jamais à les confronter à un monde physique. Contrairement à ce qui peut être dit (et surtout, ne posez pas la question aux intéressés...), il n'y a pas de hiérarchie entre mathématiques et physique. Tout le monde sait que les mathématiques sont l'outil du physicien et qu'il ne pourrait pas s'en passer, mais il serait malhonnête de penser que les mathématiques peuvent se développer en parfaite autonomie sans la physique, car elles y puisent sans cesse de nouvelles choses à théoriser pour s'enrichir. La création des nombres émane d'un besoin de pouvoir compter des ensembles d'objets, les comparer. Newton et Leibniz développent le calcul différentiel dans le cadre de leur étude des lois de la mécanique. Le développement de l'algèbre matricielle explose après avoir compris les simplifications qu'elle engendre dans les descriptions mathématiques de la mécanique quantique. Des domaines entiers de recherche mathématique s'ouvrent avec les différentes théories des cordes. Les exemples sont nombreux.
Deux-trois visions erronées du grand public vis-à-vis des théories scientifiques.
Le majeure partie du grand public ne maîtrise pas la démarche scientifique (ce qui est dit sans animosité). C'est pour cette raison que des idées erronées sur celle-ci circulent et induisent des incompréhensions. J'espère avoir aidé le lecteur à comprendre le sens d'une « théorie vraie » et d'une « théorie fausse ». En toute rigueur, on ne devrait parler que de théorie compatible, ou non, mais l'usage au quotidien finit toujours par prendre le dessus. Je voudrais maintenant montrer la portée que peut avoir cette confusion.
Imaginez que l'on dispose d'une loi qui fonctionne admirablement bien, qui est omniprésente en sciences, et qui dure depuis des siècles. Le niveau technologique ne faisant que s'élever, de nouvelles observations toujours plus poussées peuvent être réalisées et confrontées à cette loi. Et petit à petit, des problèmes apparaissent. Petit à petit, les modèles ne parviennent plus à décrire correctement ce qui est observé. Ils ne se trompent pas forcément de beaucoup, mais rien n'y fait, aucune des hypothèses que l'on a pu imaginer ont réconcilié théorie et expérience. Ces anomalies s'accumulent et on les répertorie dans un coin de la mémoire collective en attendant que quelqu'un parvienne à les expliquer. Et puis, au détour d'un problème conceptuel, on découvre que, pour le résoudre, il est nécessaire de remanier cette loi et de bouleverser la vision du monde qui l'accompagne. À partir du moment où on accepte cette nouvelle vision du monde, les anomalies disparaissent.
Ce scénario n'a rien d'abstrait, c'est une situation qui s'est déjà produite. La loi en question était la seconde loi de Newton, qui est LE pilier de la mécanique, et la théorie qui l'a remaniée est la relativité (restreinte, puis générale). C'est un cheminement que je détaille dans cet article. Pour une bonne part de la population, un tel scénario est une catastrophe. Je suis en effet en train de dire que plusieurs siècles de connaissance humaine reposent sur une loi qui se révèle être fausse ? L'édifice s'écroule ! Évidemment, à la lumière de cet article, cette réaction ne peut pas convenir. D'ailleurs, vous savez exactement pourquoi j'ai utilisé l'italique juste au-dessus. Bref, cette réaction ne peut pas convenir car en quoi cette découverte remettrait en cause les résultats de ces derniers siècles ? Si les expériences étaient compatibles avec les modèles de cette époque, c'est un fait ! Cela veut dire que les modèles suffisent et que nous n'avions pas à chercher plus loin. Quand nous avons commencé à observer de nouveaux phénomènes inexplicables, nous étions soudain en train de nous écarter du domaine de validité de notre loi, mais puisque cette loi marchait jusqu'alors, nous ne connaissions pas encore ce domaine de validité. La théorie de la relativité généralise (entre autres) la seconde loi de Newton. Autrement dit, la relativité établit des prédictions correctes là où la 2nde loi échoue, mais elle n'entre jamais en conflit avec la 2nde loi lorsque celle-ci suffit. Elle englobe entièrement les résultats de la 2nde loi. Si mathématiquement, on spécifie dans la théorie de la relativité que l'on reste dans le domaine de validité de la 2nde loi, alors la relativité elle-même se réexprime pour redonner la 2nde loi. Voilà pourquoi l'édifice, loin de s'écrouler, s'est incroyablement renforcé, tout en offrant une nouvelle vision du monde !
Cet exemple est une occasion parfaite de rebondir sur une autre idée trompeuse : le fait qu'une théorie qui échoue est une mauvaise chose. À partir de quel moment la relativité peut-elle prendre son essor ? À partir du moment où les autres échouent ! Toute anomalie qui persiste à ne pas pouvoir être expliquée par l'ensemble des lois et principes communément admis est un indice quant à un nouveau principe à formuler, ainsi qu'un terrain d'expérimentation pour le mettre à l'épreuve. Lorsque le LHC (Large Hadron Collider), l'accélérateur de particules du CERN, avait acquis suffisamment de données pour conclure quant à l'existence ou non d'une nouvelle particule, le boson de Higgs, les chercheurs n'étaient pas excités par l'idée d'avoir une réponse positive, mais par celle d'avoir une réponse tout court ! Car cela constituait ou bien une extension du domaine de validité de ce que l'on appelle le Modèle Standard (modèle qui décrit l'existence des particules subatomiques), ou bien le premier signe de sa défaillance, laissant le champ libre à d'autres théories alternatives.
Je mets l'accent sur ce détail, même si je pense que vous l'aurez compris tout au long de cet article : une théorie, en sciences, n'est pas ce terme très connoté du quotidien. Une théorie, ce n'est pas quelque idée floue et fumeuse qui vient d'on ne sait où et qui est détachée du reste. Si vous ne voyez pas de quoi je parle, pensez aux phrases du style « Oui, en théorie, ça marche comme ça, mais en pratique ça n'a rien à voir ! ». Une théorie est une construction complète qui réunit un certain nombre de lois, de principes, d'équations fondamentales, de modèles et d'observations.
J'aimerais finir cet article sur cette question : à votre avis, qui élabore des théories ? Ma réponse, c'est tout le monde. C'est un procédé qui est si commun que vous n'en avez pas forcément conscience. Évidemment, vous ne mesurez pas toujours quelque chose et vous ne posez pas d'équations, mais vous raisonnez à partir d'hypothèses, de constatations issues de votre expérience du quotidien, parfois de calculs afin d'en tirer une conclusion, qu'elle soit quantitative ou qualitative. La théorie n'est donc absolument pas l'apanage des scientifiques, c'est simplement le procédé naturel qui permet de faire coller votre représentation du monde au monde lui-même pour en prédire quelque chose. Et évidemment, puisque la théorie est le cœur de métier du scientifique, celui-ci connaît son fonctionnement explicitement et non pas uniquement intuitivement.